This blog summarizes the query graphs that are frequently used in isomorphism-based subgraph matching algorithm/system research. The surveyed literature is listed in the “Reference” section.
Problem Definition of Isomorphism-based Subgraph Matching
Given a single large data graph $D$ and a small query graph $q$, the target of subgraph isomorphism is to find all subgraphs of $D$ that are isomorphic to $q$.
The data graph and query graph may have labels attached to the vertices and/or edges. In those cases, a subgraph of $D$ matches the query graph $q$ if and only if they are isomorphic and their corresponding vertex/edge labels match.
Classification of Query Graphs
The query graphs used in the experiments of related literature can be classified into three groups: sampled queries, fixed queries and derived queries.
- Fixed Queries: The topology of fixed queries is determined in advance, independent of data graphs. They are widely-used in experimental evaluation on unlabeled graphs.
- Sampled Queries: The topology of sampled queries is sampled from the data graph. Sampled queries are widely-used in experimental evaluation on labeled graphs.
- Derived Queries: The topology of derived queries are retrieved from query statements of database benchmarks. Derived queries are tightly bound with the data graphs of the benchmarks.
Fixed Queries
The topology of fixed query graphs are given in advance which is independent of the data graphs.
Undirected Unlabeled Queries
The following figure summarizes the widely-used fixed undirected unlabeled query graphs and gives each query graph a short code name. The symmetry-breaking conditions are also listed under the corresponding query graphs.
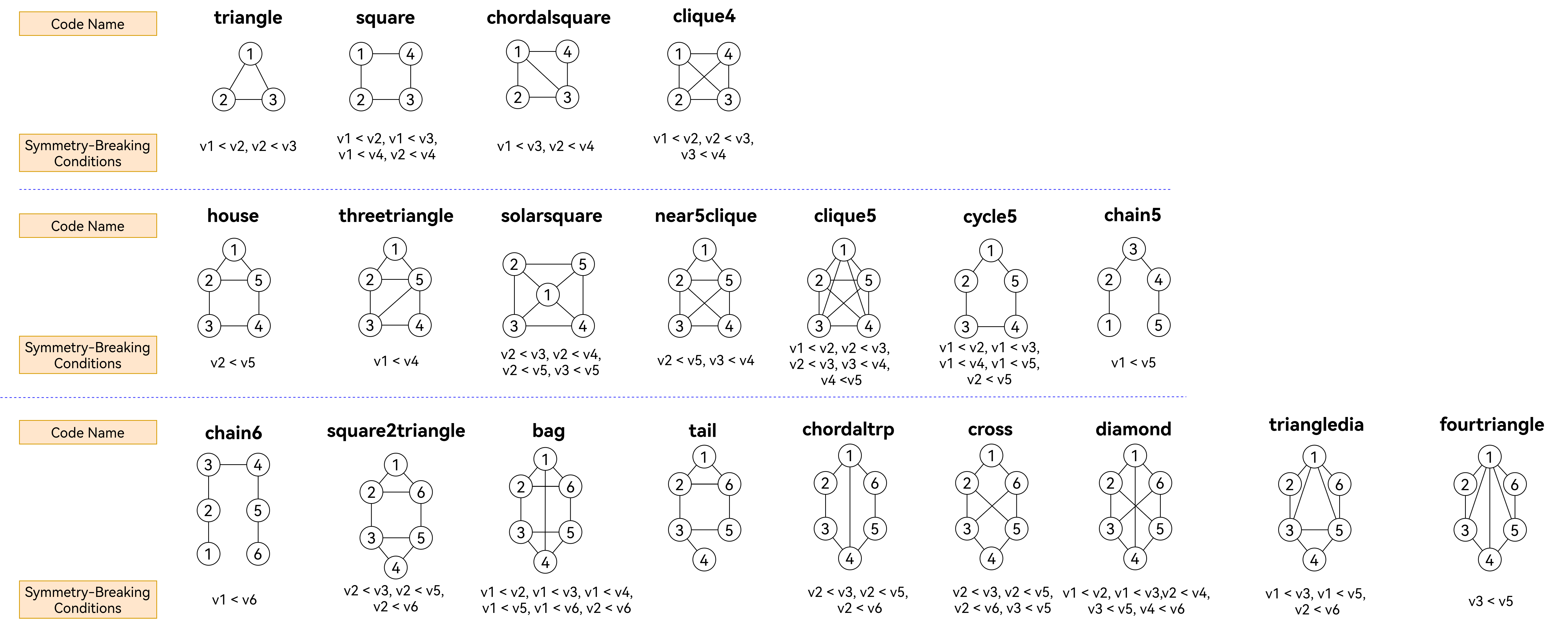
For undirected unlabeled query graphs, I provide a program calc_symmetry_breaking_conditions.py to calculate the symmetry-breaking conditions for a given query graph.
The following research work uses many query graphs in the experimental evaluation. The authors group the query graphs into different groups:
- Park et al. [13] use a group of fixed patterns to generate query graphs with different sizes: chain, star, tree, cycle, clique, petal, flower, and graph.
- Zhang et al. [8] use 114 query graphs from PTE, BENU, ECLOG, and JESSE. The Fig. 10 of [8] shows typical query graphs of each group.
Directed Queries
Mhedhbi and Salihoglu [18] propose 14 directed unlabeled query graphs in Fig. 6. For the labeled graphs, they assign random labels to edges and vertices of query graphs.
Zhu et al. [24] propose a group of 12 directed query graphs in its Fig. 7. The edge labels are assigned uniformly in a random manner.
Sampled Queries
The sampled queries are gotten by conducting random walk in the data graph. Given the number of vertices $i$ in the query graph, the random walk has three steps:
- select a vertex of the data graph uniformly at random;
- conduct random walk from the selected vertex until the random walk visits $i$ vertices;
- extract a subgraph from the visited vertices and the visited (or induced) edges.
The sampled subgraphs are usually divided into two categories according to their average degrees:
- Sparse queries: the average degree of the sampled graph is less than or equal to 3;
- Dense queries: the average degree of the sampled graph is bigger than 3.
For a given number of vertices $i$, many query graphs are generated to form a query set. For each query set, the average querying time of all queries in the query set is reported in the experimental results.
Derived Queries
Derived query graphs are derived from the standard query statements provided by some benchmarks (like LDBC-SNB and LUBM). The query statements are written with query languages like SPARQL or Cypher. The query graphs are retrieved manually from the query statements.
LUBM: Q2, Q4, Q7, Q8, Q9 and Q12 (from [13]).
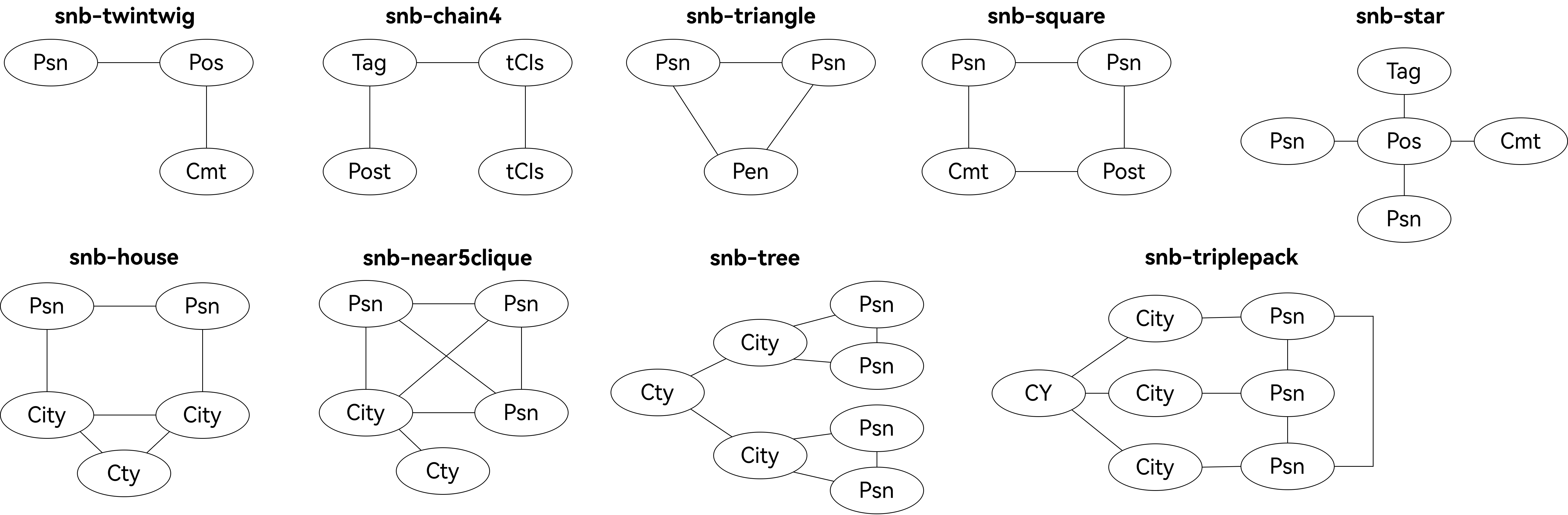
LDBC-SNB: Lai et al. [17] derive a group of fixed undirected labeled query graphs for the LDBC-SNB benchmark as shown below.
References
- C. T. Duong, D. Hoang, H. Yin, M. Weidlich, Q. V. H. Nguyen, and K. Aberer, “Efficient Streaming Subgraph Isomorphism with Graph Neural Networks,” Proc. VLDB Endow., vol. 14, no. 5, pp. 730–742, 2021.
- X. Jin, Z. Yang, X. Lin, S. Yang, L. Qin, and Y. Peng, “FAST: FPGA-based Subgraph Matching on Massive Graphs,” in Proc. ICDE, 2021, pp. 1452–1463. doi: 10.1109/ICDE51399.2021.00129.
- D. Mawhirter, S. Reinehr, C. Holmes, T. Liu, and B. Wu, “GraphZero: A High-Performance Subgraph Matching System,” SIGOPS Oper. Syst. Rev., vol. 55, no. 1, pp. 21–37, 2021, doi: 10.1145/3469379.3469383.
- H. Kim, Y. Choi, K. Park, X. Lin, S.-H. Hong, and W.-S. Han, “Versatile Equivalences: Speeding up Subgraph Query Processing and Subgraph Matching,” in SIGMOD, New York, NY, USA, 2021, pp. 925–937. doi: 10.1145/3448016.3457265.
- Z. Yang, L. Lai, X. Lin, K. Hao, and W. Zhang, “HUGE: An Efficient and Scalable Subgraph Enumeration System,” in Proc. SIGMOD, New York, NY, USA, 2021, pp. 2049–2062. doi: 10.1145/3448016.3457237.
- W. Guo, Y. Li, M. Sha, B. He, X. Xiao, and K.-L. Tan, “GPU-Accelerated Subgraph Enumeration on Partitioned Graphs,” in Proc. SIGMOD, New York, NY, USA, 2020, pp. 1067–1082. doi: 10.1145/3318464.3389699.
- S. Sun and Q. Luo, “In-Memory Subgraph Matching: An In-Depth Study,” in SIGMOD, New York, NY, USA, 2020, pp. 1083–1098. doi: 10.1145/3318464.3380581.
- H. Zhang, J. X. Yu, Y. Zhang, K. Zhao, and H. Cheng, “Distributed Subgraph Counting: A General Approach,” Proc. VLDB Endow., vol. 13, no. 11, pp. 2493–2507, 2020.
- X. Jian, Y. Wang, X. Lei, Y. Shen, and L. Chen, “DDSL: Efficient Subgraph Listing on Distributed and Dynamic Graphs,” in Proc. DASFAA, Cham, 2020, pp. 632–640.
- L. Zeng, L. Zou, M. T. Özsu, L. Hu, and F. Zhang, “GSI: GPU-friendly Subgraph Isomorphism,” in Proc. ICDE, Apr. 2020, pp. 1249–1260. doi: 10.1109/ICDE48307.2020.00112.
- S. Sun, X. Sun, Y. Che, Q. Luo, and B. He, “RapidMatch: a holistic approach to subgraph query processing,” Proc. VLDB Endow., vol. 14, no. 2, pp. 176–188, Oct. 2020, doi: 10.14778/3425879.3425888.
- D. Yan, G. Guo, M. M. R. Chowdhury, M. T. Özsu, W.-S. Ku, and J. C. S. Lui, “G-thinker: A Distributed Framework for Mining Subgraphs in a Big Graph,” in Proc. ICDE, 2020, pp. 1369–1380. doi: 10.1109/ICDE48307.2020.00122.
- Y. Park, S. Ko, S. S. Bhowmick, K. Kim, K. Hong, and W.-S. Han, “G-CARE: A Framework for Performance Benchmarking of Cardinality Estimation Techniques for Subgraph Matching,” in SIGMOD, New York, NY, USA, 2020, pp. 1099–1114. doi: 10.1145/3318464.3389702.
- T. Reza, M. Ripeanu, G. Sanders, and R. Pearce, “Approximate Pattern Matching in Massive Graphs with Precision and Recall Guarantees,” in Proc. SIGMOD, New York, NY, USA, 2020, pp. 1115–1131. doi: 10.1145/3318464.3380566.
- M. Han, H. Kim, G. Gu, K. Park, and W.-S. Han, “Efficient Subgraph Matching: Harmonizing Dynamic Programming, Adaptive Matching Order, and Failing Set Together,” in Proc. SIGMOD, New York, New York, USA, 2019, pp. 1429–1446. doi: 10.1145/3299869.3319880.
- B. Bhattarai, H. Liu, and H. H. Huang, “CECI: Compact Embedding Cluster Index for Scalable Subgraph Matching,” in SIGMOD, 2019, pp. 1447–1462. doi: 10.1145/3299869.3300086.
- L. Lai et al., “Distributed subgraph matching on timely dataflow,” PVLDB, vol. 12, no. 10, pp. 1099–1112, 2019, doi: 10.14778/3339490.3339494.
- A. Mhedhbi and S. Salihoglu, “Optimizing Subgraph Queries by Combining Binary and Worst-Case Optimal Joins,” Proc. VLDB Endow., vol. 12, no. 11, pp. 1692–1704, 2019, doi: 10.14778/3342263.3342643.
- Z. Zhang, H. Wei, J. Xu, and B. Choi, “GScan: Exploiting Sequential Scans for Subgraph Matching,” in Proc. DASFAA, Cham, 2019, pp. 471–475.
- Z. Wang, R. Gu, W. Hu, C. Yuan, and Y. Huang, “BENU: Distributed Subgraph Enumeration with Backtracking-Based Framework,” in ICDE, Macao, Macao, Apr. 2019, pp. 136–147. doi: 10.1109/ICDE.2019.00021.
- D. Chakrabarti, Y. Zhan, and C. Faloutsos, “R-MAT: A Recursive Model for Graph Mining,” in Proceedings of the Fourth SIAM International Conference on Data Mining, Lake Buena Vista, Florida, USA, April 22-24, 2004, 2004, pp. 442–446. doi: 10.1137/1.9781611972740.43.
- G. Aluç, O. Hartig, M. T. Özsu and K. Daudjee. Diversified Stress Testing of RDF Data Management Systems. In Proc. The Semantic Web - ISWC 2014 - 13th International Semantic Web Conference, 2014, pages 197-212. WatDiv available from http://dsg.uwaterloo.ca/watdiv/.
- H. Park and M.-S. Kim, “EvoGraph: An Effective and Efficient Graph Upscaling Method for Preserving Graph Properties,” in Proc. SIGKDD, New York, NY, USA, 2018, pp. 2051–2059. doi: 10.1145/3219819.3220123.
- K. Zhu, G. Fletcher, and N. Yakovets, “Leveraging Temporal and Topological Selectivities in Temporal-clique Subgraph Query Processing,” in Proc. ICDE, 2021, pp. 672–683. doi: 10.1109/ICDE51399.2021.00064.